La distancia a las estrellas

Mirar al cielo nocturno es contemplar un lienzo de luces situado a una distancia que durante siglos fue un misterio inescrutable. Las estrellas, esos puntos titilantes, parecían estar fijas en una cúpula celeste mágica a alguna "altura" desconocida. Pero, ¿cómo se logró romper esa ilusoria frontera y medir cómo de lejos se encuentran realmente las estrellas? Este es el relato de un hito en la historia de la Astronomía: el descubrimiento de cómo medir la distancia a las estrellas.

El reto de medir distancias en el cielo

Durante siglos los astrónomos intentaron determinar las distancias a las estrellas utilizando el paralaje estelar, un método que aprovecha el movimiento de la Tierra alrededor del Sol para observar pequeños desplazamientos en la posición aparente de una estrella frente al fondo estelar más lejano. Sin embargo, estas variaciones son tan diminutas que los instrumentos antiguos eran incapaces de detectarlas. El obstáculo principal era la precisión de los telescopios y no fue sino hasta bien entrado el siglo XIX cuando los avances en óptica y métodos de observación permitieron llevar este método a la práctica.

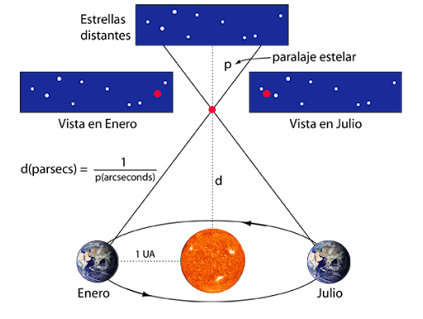Método del paralaje estelar

Friedrich Bessel y la estrella 61 del Cisne

El momento clave llegó en 1838, cuando Friedrich Wilhelm Bessel, matemático y astrónomo prusiano, logró medir la distancia a una estrella: en concreto a 61 del Cisne. Esta estrella doble era una candidata ideal porque su movimiento propio, su desplazamiento aparente en el cielo, (ver artículo anterior) era notablemente rápido, lo que sugería que la estrella estaba relativamente cerca.

Bessel utilizó el heliómetro de Fraunhofer (sí, el mismo físico conocido por las Líneas de Fraunhofer y muchas otras aportaciones a la Ciencia), un instrumento que permitía medir ángulos con una precisión extraordinaria. Durante meses, registró cómo cambiaba la posición aparente de la estrella en función de la órbita terrestre. Finalmente, calculó que el paralaje de 61 del Cisne era de 0,314 segundos de arco, lo que situó a la estrella a unos 10,3 años luz de distancia. Éste fue el primer cálculo exitoso de la distancia a una estrella más allá del Sol.

Este resultado confirmó además, por primera vez, la hipótesis de Giordano Bruno sobre la inmensidad del universo y la posibilidad de que las estrellas fueran soles lejanos con planetas habitables orbitando a su alrededor. 

Bruno, Fraunhofer y Bessel en una representación de ChatGPT,
basada en retratos disponibles de los tres científicos. 

El Parsec

Gráfico de definición de Parsec

Aprovecharemos ahora para recordar que muchas veces los astrónomos no miden las distancias en años-luz sino en parsecs. Con lo que hemos comentado en el párrafo anterior ahora podemos entender perfectamente qué es eso del parsec: Un parsec es la distancia a la cual se situaría una estrella que en una UA (unidad astronómica: distancia media de la Tierra al Sol) describiera un PARalaje de un SEGundo de arco (SECond en inglés), de ahí par-sec.

De esta forma un PAR-SEC es el equivalente a 3.26 años luz o 30 856 804 799 935 500 metros.

El uso del parsec nace de forma natural del método de Bessel, así la distancia se puede calcular simplemente como el recíproco (o inverso) del ángulo en segundos de arco. Por ejemplo si el ángulo medido es 0.4 segundos de arco, el objeto estará a 1 / 0.4 = 2.5 parsecs.

Otras estrellas cercanas

Tras el logro de Bessel, otros astrónomos también midieron distancias estelares. En el mismo periodo, Thomas Henderson determinó el paralaje de Alfa Centauri, nuestro sistema estelar vecino: 0,75 segundos de arco, lo que resultó en una distancia de 4,3 años luz hasta nosotros, siendo el sistema estelar más cercano a la Tierra. Friedrich Struve midió la distancia hasta Vega y la situó a unos 25 años luz de distancia. Cada nueva medida confirmaba que las estrellas estaban a distancias inconcebibles para los estándares terrestres. Y apenas se estaban midiendo las distancias a las estrellas más inmediatas.

La relevancia de medir distancias

El trabajo de Bessel abrió las puertas a una nueva era en astronomía. Saber cuan lejos están las estrellas no solo nos da una idea de las dimensiones del Cosmos, sino que también nos permite calcular sus luminosidades reales, tamaños y otras propiedades físicas.

Hoy en día, con misiones como la europea GAIA, que mapea la Vía Láctea con una precisión sin precedentes, seguimos ampliando nuestro conocimiento sobre las distancias estelares. Sin embargo, el método del paralaje sigue siendo la piedra angular de este esfuerzo, tal como lo demostró Bessel hace casi dos siglos.

Recreación artística del Satélite GAIA de la ESA

Conclusión

El viaje para medir la distancia a las estrellas es un ejemplo de cómo la humanidad ha superado límites técnicos y conceptuales para desentrañar los misterios del universo. Desde los modestos instrumentos de Bessel hasta los sofisticados satélites actuales, seguimos mirando al cielo con la misma pregunta fundamental: ¿cómo de lejos están las estrellas? 

Tanto para ésta como para el resto de las preguntas que nos hacemos los curiosos, recordad que estos artículos son tan solo una introducción; Internet está lleno de recursos magníficos para profundizar en cualquier tema de vuestro interés. No desaprovechéis el acceso al conocimiento del que ninguna otra generación de apasionados por la Ciencia pudo gozar.

Y recuerda también que cada vez que alzamos la vista al cielo nocturno, no solo contemplamos las estrellas, sino también el legado de siglos de ingenio humano que nos permite comprender su lugar en el Cosmos.

El Sistema Solar es... graaaaaande! (Segunda Parte) y alguna cosa más.

Retomemos el viaje que iniciamos en un artículo anterior para recorrer nuestro Sistema Solar en un modelo a escala que, recordemos, situaba al Sol como una esfera de 2 metros de diámetro en la plaza de Cózar. Habíamos llegado al Cinturón de Asteroides y es hora de alejarnos hasta el más grande de los planetas, algunas veces denominado como una estrella fallida, su majestad celestial Júpiter, al que encontraremos en el camino del Cementerio, a 1 Kilómetro y 120 metros del Sol, representado por una pelota de 20 centímetros de diámetro, como esas pequeñas pelotas de gomaespuma con las que juegan niñas y niños pequeños.

Comparativa Júpiter, Tierra-Luna, Io.

Pero miremos con atención en los alrededores de la pelota y veremos cantidad de pequeñas, pequeñísimas bolitas. Cuatro de ellas podrían llamar nuestra atención, son las lunas de Galileo, los cuatro satélites principales de Júpiter observados por primera vez por el padre de la Física Moderna. Son Io, una bolita de 5,2 milímetros de diámetro a 60 centímetros de Júpiter; Europa, de 4,5 milímetros, más pequeña que nuestra Luna, a casi 1 metro de la pelota de goma; Ganímedes, de 8 milímetros, a metro y medio del Planeta Rey, siendo así el mayor de todos los satélites del Sistema Solar; y Calisto, de 7 milímetros a 2 metros y 70 centímetros de nuestro Júpiter de goma.

Es hora de dirigirnos al planeta favorito de la observación astronómica, Saturno y sus anillos. Para encontrarlo tendremos que tomar el Camino de la Casa del Monte y a 2 Kilómetros del Sol, al poco de pasar la curva a la izquierda de este camino marcada por una vieja señal, encontraremos una pelota de 16,7 centímetros de diámetro. Es una pelota algo especial porque la rodean tres aritos a unos 3, 5 y 9 centímetros de su superficie. Además, a metro y 75 centímetros del centro de Saturno veremos otra bolita, de 7,4 milímetros de diámetro, Titán, el segundo mayor satélite del Sistema Solar.

Saturno fotografiado por Cassini-Huygens

Dejamos atrás las dos mayores atracciones de nuestro hogar en la Vía Láctea y toca ahora armarse de paciencia para alcanzar los dos otros gigantes del Sistema. Localizamos a Urano a 4 Kilómetros y 130 metros del Sol, justo en el cruce entre las carreteras de Torrenueva y Valdepeñas, representado por una pelota de 7,3 centímetros, algo mayor que una pelota de tenis. Finalmente llegaremos a Neptuno si nos alejamos a 6 Kilómetros y 470 metros del Sol, por ejemplo en las ruinas de Xamila, ya en Infantes, y lo reconoceremos como otra pelota de tenis algo sobredimensionada de 7 centímetros de diámetro. A medio metro de Neptuno repararemos en una bolita de 4 milímetros de diámetro, es Tritón, su satélite principal.

A continuación podemos ver la representación en Google Maps del Sistema Solar Exterior Cozareño:

Sistema Solar centrado en Cózar.

Ah, pero, ¿todavía queréis ir más lejos? Recordad que nuestro modelo se ha originado tomando como referencia el Sol, transformado en una gran esfera de 2 metros de diámetro, lo que indica que estamos usando la escala 1:696.000.000, en la que 1 metro representa 696,000 Kilómetros, y con esta gigantesca escala para llegar a Neptuno estamos ya a las puertas de Villanueva de los Infantes. 

¿Dónde podríamos encontrar a Plutón, el planeta enano que domina la región llamada Cinturón de Kuiper? Tendríamos que alejarnos a 8,4 kilómetros del Sol, más o menos en el centro de Torre de Juan Abad. Y para alcanzar Eris, el mayor planeta enano descubierto hasta ahora en el Disco Disperso, nos alejaremos a 14,6 Kilómetros, como al extremo sur de Villamanrique. En el propio Disco quedarían incluidas Almedina, Santa Cruz de los Cáñamos, Puebla del Príncipe, Montiel, Villahermosa, parte de Infantes (la otra parte en el Cinturón de Kuiper), parte de Carrizosa, Alcubillas, Pozo de la Serna, el embalse de La Cabezuela y la mismísima Cabeza del Buey, rozando Castellar de Santiago, prácticamente la comarca entera del Campo de Montiel. Veámoslo en el mapa:

Cinturón de Kuiper y Disco Disperso con centro en Cózar.

Hemos llegado a los límites convencionales del Sistema Solar pero no nos queremos despedir sin algunos otros datos interesantes que nos ayuden a imaginar la inmensidad del Cosmos.

Si en nuestro modelo quisiéramos representar Alpha Centauri, la estrella (en realidad una estrella triple) más cercana a nuestro Sol y situada a 4,4 años luz (más de 41 billones de kilómetros) tendríamos que hacerlo a casi 60.000 kilómetros de Cózar. Puesto que no hay nada sobre la superficie de la Tierra a tanta distancia, para situar nuestra esfera, en este caso de 2,5 metros de diámetro que representara a Alpha Centauri, nos tendríamos que subir a una nave espacial que nos llevara al límite convencional de la magnetosfera, campo magnético que rodea la Tierra y la protege de partículas cargadas procedentes del Sol.

Andrómeda, un billón de bolitas :)

¿Y si queremos llegar al centro de nuestra galaxia en nuestro modelo? Dicho centro se situa a unos 25.000 años luz, por lo que en nuestro modelo tendríamos que viajar a 337 millones de kilómetros, es decir más allá del Cinturón de Asteroides. 

Tomemos aire para recapacitar, situando el Sol en el centro de nuestro pueblo, representado por una pelota de 2 metros, para representar el centro de la Via Lactea tendríamos que viajar más allá de Ceres, acercándonos a la órbita de Júpiter.

Y para acabar de reventar nuestra capacidad de imaginar, ¿dónde tendríamos que situar, en nuestro modelo, nuestra galaxia hermana Andrómeda, que en realidad está a 2 millones y medio de años luz? Nada más fácil, vayamos a 35 mil millones de kilómetros de la Tierra, es decir acerquémonos a la Alpha Centauri real, cosa que ninguna nave ha hecho jamás ni de lejos, y coloquemos allí un billón de globos. Si has llegado hasta aquí recuerda que, a escala cósmica, apenas hemos dado un solo paso.